Foreword
This is the documentation of the Trail parser generator.
Trail is a parser generator for top down parsers based on a method I
have called trace based parsing.
Trace based parsing extends a parsing scheme that is known since Ken
Thompsons work [1] of the late 60s about parsing
regular expressions using nondeterministic finite atutomata (NFAs). It
is used in Trail to parse languages using general context free grammars
in EBNF format. For LL(1) grammars trace based parsing collapses to NFA
driven LL(1) parsing with O(n) complexity on the length of the input
token stream. For non left factored grammar rules Trail modifies LL(1)
parsing by carefully embedding NFA transition tables into each other.
This step is called NFA expansion.This
way Trail achieves the power of advanced lookahead schemes or
backtracking parsers with one token of lookahead. The effort of trace
based parsing can grow considerably with the size of the expanded NFAs.
Improved parsers using expanded NFAs remain to be investigated in the
future.
1. Introduction
Top down parsers of context free languages generally suffer from
following issues
- Left recursion. A rule might be written in the style S: digit | S '+' S |
S '*' S . A top down parser finding a digit has
several choices to continue the parse. This can usually be avoid by
transforming the rule into a right recursive style with various efforts.
- Ambiguities. It is known that no algorithm is possible used
to detect all ambiguities of
a grammar. However detection schemes have been studied. Trail ignores
this problematic completely. It doesn't use an intelligent
disambiguation scheme either. So if you have a language with an
ambigous grammar e.g. C and want to write a parser, Trail can be a
pre-parser at best.
- Left factoring. A grammar rule S might have the
structure S = A S1 | A S2. We have to examine each branch in
order to know whether a string matches against A S1 or A S2. This can
become quite costly e.g. when S' = A* S1 | A* S2. An obvious solution
in simple cases is to factor A* out: S' = A* ( S1 | S2 ). But then S1
and S2 still may have common FIRST_SETs and only through expansion of
S1 and S2 we can reproduce the simple structure we observe in S or S'.
In practice left factoring in top-down parsing is the most pressing
problem. Programmers run very frequently in a situation where they
define a rule
S = A | B and where A and B can both match a terminal t. The most frequent strategies to
solve this problem are
1) Backtracking.
Here we check if A can fully match an initial
section of the token sequence T = (t1, t2, ... ). If so a parse tree
with A as the root node is yielded.
Otherwise we checkout the same with B. If neither A
nor B match T an error will be reported.
Backtracking is very simple and universally
applicable but it can be very costly.
2) Lookahead.
This is best
explained
by Terrence Parr the creator of ANTLR
that can look arbitrary
deep into a token stream for disambiguation purposes.
A third method is used by Trail. It's a combination of two methods.
1) Parallel NFA traversal. A grammar is transformed into a NFA. The NFA
will be traversed in parallel: when S = A B ... x | A B ... y both
branches will be examined at the same time.
2) Expansion. When S = A | B, A=! B and A and B have common FIRST_SETs
then A and possibly also B will be expanded into their
subrule structures. Expansion will be repeated until
S has the simple structure described in 1) or a cycle occurs that
indicates left recursion.
In that case expansion will be stopped with a
warning.
2. Using
Trail
Trail based lexers and parsers are implemented in the EasyExtend/trail
package. One can directly import NFAParser and CFAParser objects.
However it is required to pass a langlet
argument into NFALexers and NFAParsers and for langlets there exist
simpler ways to use parsers and lexers.
2.1 Import
NFALexer and NFAParser
>>> import EasyExtend.langlets.zero.langlet as langlet
>>> from EasyExtend.trail.nfalexer import NFALexer, TokenStream
>>> lexer = NFALexer(langlet)
>>> lexer.scan(TokenStream("1+2"))
[[(258, 'NUMBER'), '1', (1, 1), (0, 1)], [(270, 'PLUS'), '+', (1, 1), (1, 2)], [(258, 'NUMBER'), '2', (1, 1), (2, 3)]]
>>>
|
The input TokenStream is just a wrapper around the source string. The
idea of passing a token stream into a lexer might feel strange but the
lexer is just another Trail parser with some special properties.
In the EasyExtend framework the output token stream of the scan()
method is not be passed immediately to the Trail parser. Instead it has
to run through a filtering or postprocessing step. In this process
token for significant whitespace are created for Python. The specific
or context sensitive part of lexical analysis is implemented in
eetokenizer.py and can be overridden.
For doing a proper analysis we have to do the following steps
>>>
from EasyExtend.eetokenizer import Tokenizer
>>> tokenizer = Tokenizer(langlet)
>>> tokenizer.tokenize_string("def f():\n print 77")
[[1, 'def', 1, (0, 3)], [1, 'f', 1, (4, 5)], [7, '(', 1, (5, 6)], [8,
')', 1, (6, 7)], [11, ':', 1, (7, 8)], [4, '\n', 1, (8, 8)], [5,
' ', 2, (0, 2)], [1, 'print', 2, (2, 7)], [2, '77', 2, (8, 10)],
[6, '', 3, (0, 0)], [0, '', 4, (0, 0)]]
|
Among other things this tokenstreams contains the token [5, ' ', 2,
(0, 2)] which represents an INDENT token and [6, '', 3, (0, 0)]
which is the complementary DEDENT.
2.2 Using Trail
functions from langlets
If you are acting inside the context of a langlet Trail is already
actively used. However you can also access it explicitely e.g. for test
purposes:
c:\lang\Python25\Lib\site-packages\EasyExtend\langlets\zero>python
run_zero.py
__________________________________________________________________________________
zero
On Python 2.5.1 (r251:54863, Apr 18 2007, 08:51:08) [MSC v.1310
32 bit (Intel)]
__________________________________________________________________________________
>>>
>>> parse("zero")
[258, [326, [303, [304, [305, [306, [307, [309, [310, [311, [312, [313,
[314, [315, [316, [317, [1, 'zero', 1]]]]]]]]]]]
]]]]], [0, '', 2]]
>>> tokenize("def f():\n print 77\n")
[[1, 'def', 1, (0, 3)], [1, 'f', 1, (4, 5)], [7, '(', 1, (5, 6)], [8,
')', 1, (6, 7)], [11, ':', 1, (7, 8)], [4, '\n', 1, (8, 8)], [5,
' ', 2, (0, 2)], [1, 'print', 2, (2, 7)], [2, '77', 2, (8, 10)],
[4, '\n', 2, (10, 10)], [6, '', 3, (0, 0)], [0, '', 4, (0, 0)]]
>>> parse("def f():\n print 77\n")
[257, [266, [291, [261, [1, 'def', 1], [1, 'f', 1], [262, [7, '(', 1],
[8, ')', 1]], [11, ':', 1], [299, [4, '\n', 1], [5, ' ', 2],
[266, [267, [268, [271, [1, 'print', 2], [303, [304, [305, [306, [307,
[309, [310, [311, [312, [313, [314,[315, [316, [317, [2, '77',
2]]]]]]]]]]]]]]]]], [4, '\n', 2]]], [6, '', 3]]]]], [0, '', 4]]
>>>
>>> pprint(parse("def f():\n print 77\n"))
file_input -- S`257 -- 257
stmt -- S`266 -- 266
compound_stmt -- S`291 -- 291
funcdef -- S`261 -- 261
NAME -- T`1 --
1 L`1
def
NAME -- T`1 --
1 L`1
f
parameters -- S`262 --
262
LPAR --
T`7 -- 7 L`1
(
RPAR --
T`8 -- 8 L`1
)
COLON -- T`11 --
11 L`1
:
suite -- S`299 -- 299
NEWLINE --
T`4 -- 4 L`1
'\n'
INDENT --
T`5 -- 5 L`2
stmt --
S`266 -- 266
simple_stmt -- S`267 -- 267
small_stmt -- S`268 -- 268
print_stmt -- S`271 -- 271
NAME -- T`1 -- 1 L`2
print
test -- S`303 -- 303
or_test -- S`304 -- 304
and_test -- S`305 -- 305
not_test -- S`306 -- 306
comparison -- S`307 -- 307
expr -- S`309 -- 309
xor_expr -- S`310 -- 310
and_expr -- S`311 -- 311
shift_expr -- S`312 -- 312
arith_expr -- S`313 -- 313
term -- S`314 -- 314
factor -- S`315 -- 315
power -- S`316 -- 316
atom -- S`317 -- 317
NUMBER -- T`2 -- 2 L`2
77
NEWLINE -- T`4 -- 4 L`2
'\n'
DEDENT --
T`6 -- 6 L`3
''
ENDMARKER -- T`0 -- 0 L`4
''
|
3. Trail
design fundamentals
In the initial and preparational step we translate grammar rules into
nondetermninistic finite automata ( NFAs ). Those NFAs have a simple
visualization as syntax diagrams.
Example:
The following grammar rule describes the argument
list for a function call in Python 2.5
-
arglist
|
::= |
(argument
',')* (argument [',']| '*' test [',' '**' test] | '**' test)
|
Below is the corresponding syntax diagram:
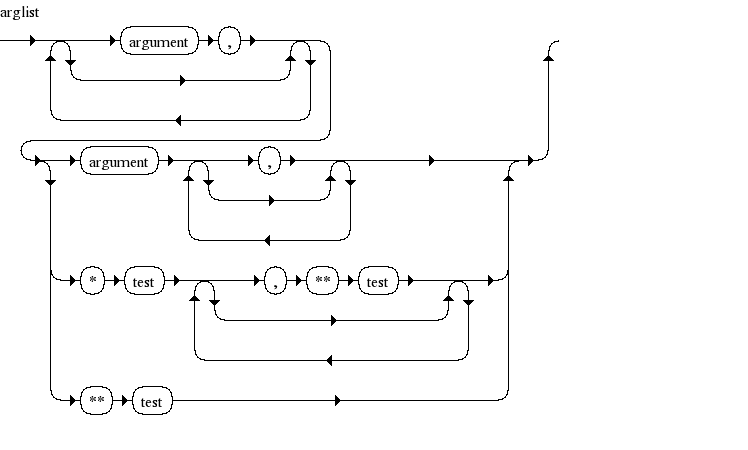
( Image 1: generated with syntax diagram generator being
available here
).
Each node in the syntax diagram corresponds either with a
terminal or
nonterminal of the language grammar. For each of those
terminals/nonterminals Trail uses a
numerical encoding [2].
For the graph above we have following encoding scheme:
Token/Symbol name
|
Python 2.5 numerical code
|
arglist
|
329
|
argument
|
330
|
test
|
303
|
',' (
COMMA )
|
12
|
'*'
( STAR )
|
16
|
'**' (
DOUBLESTAR )
|
36
|
We call the
numerical codes node ids. A trace through the NFA corresponds
to a valid trace through the diagram. This can always be represented by
a sequence of symbols of the diagram.We chose None as an explicit
symbol of trace termination.
Example:
Symbol sequence
|
Corresponding node id sequence
|
argument ',' argument None
|
330 12 330 None
|
argument ',' '**' test None
|
330 12 36 303 None
|
'**' test None
|
36 303 None
|
3.1 Labels
Different instances of COMMA, test
or argument
are mapped onto different locations in the syntax diagram. Just using
node ids isn't sufficient to encode those different locations. We use
an arbitrary indexing scheme instead. In the diagram we see three
different instances of test
at three different locations. We can just enumerate them and create
tuples (303,
1), ( 303, 2), (303, 3).
The index has no significance other than distinguishing those node ids
from each other. The tuples are called node labels or labels for short. A special label
is used for None. None is the unique exit symbol and the corresponding
label is (None,
'-').
3.2 Transitions
Each transition in the diagram is encoded in terms of labels. Each
label can have one or more follow labels. The only exception is the
exit label (None,
'-') which is the only one that has no follow labels and must
be present at least one time. A complete translation of the syntax
diagram into label transitions is shown below.
"arglist:
( argument ',' ) * ( argument[ ',' ] | '*' test[ ',' '**' test ] | '**'
test )",
(329, 0),
{(12, 2): [(16, 5),
(330, 3),
(330, 1),
(36, 10)],
(12, 4): [(None, '-')],
(12, 7): [(36, 8)],
(16, 5): [(303, 6)],
(36, 8): [(303, 9)],
(36, 10): [(303, 11)],
(303, 6): [(12, 7), (None,
'-')],
(303, 9): [(None, '-')],
(303, 11): [(None, '-')],
(329, 0): [(16, 5),
(330, 3),
(330, 1),
(36, 10)],
(330, 1): [(12, 2)],
(330, 3): [(12, 4), (None,
'-')]}],
|
The label (329,
0) is the start label. Each trace through the diagram can be
expressed as a sequence of labels beginning with (329, 0)
and ending with (None, '-').
Trail translates each grammar rule into such a nfa label
transition table.
3.3 Extending
Labels
We will later introduce expansion techniques for NFA label transition
tables. This might eventually lead to embedding of one NFA transition
table into another one. In those cases the distinctions we just made
between node ids in one NFA are not sufficient. Instead we have to make
each node id unique in the complete set of NFAs. We do this by
extending the labels. This is done by just appending the node id of the
start label of the NFA to each of the labels. In case of arglist
the node id of the start symbol was 329 and we create new labels
(329,
0, 329), (330, 1, 329), ( 330, 3, 329), (36, 10, 329), ...
from the old ones.
Note that (None,
'-') loses its uniqueness and becomes extended as well. The
exit symbol of one NFA doesn't correspond with the exit symbol of
another one. So it makes sense to write (None, '-', 329).
The new NFA transition tables looks like this:
"arglist:
( argument ',' ) * ( argument[ ',' ] | '*' test[ ',' '**' test ] | '**'
test )",
(329, 0, 329),
{(12, 2, 329): [(16, 5, 329),
(330, 3, 329),
(330, 1, 329),
(36, 10, 329)],
(12, 4, 329): [(None, '-',
329)],
(12, 7, 329): [(36, 8, 329)],
(16, 5, 329): [(303, 6,
329)],
(36, 8, 329): [(303, 9,
329)],
(36, 10, 329): [(303, 11,
329)],
(303, 6, 329): [(12, 7,
329), (None, '-', 329)],
(303, 9, 329): [(None, '-',
329)],
(303, 11, 329): [(None, '-',
329)],
(329, 0, 329): [(16, 5, 329),
(330, 3, 329),
(330, 1, 329),
(36, 10, 329)],
(330, 1, 329): [(12, 2,
329)],
(330, 3, 329): [(12, 4,
329), (None, '-', 329)]}],
|
4. Trace based
parsers
4.1 A
simple parse tree checker using label traces
We can now generalize simple node id sequences representing sequences
of terminal + nonterminal sequences to label traces:
Symbol sequence
|
Corresponding label trace
|
argument None
|
(329,0,329) (330,3,329)
(None,'-',329)
|
argument ',' None
|
(329,0,329) (330,3,329)
(12, 4, 329) (None, '-', 329) |
argument ',' argument None
|
(329,0,329) (330,1,329)
(12, 2, 329) (330,3,329) (None, '-', 329) |
When projecting the label traces onto node id sequences we get:
| Label trace |
Node id projection
|
| (329,0,329) (330,3,329)
(None,'-',329) |
329 330 None
|
| (329,0,329) (330,3,329)
(12, 4, 329) (None, '-', 329) |
329 330 12 None |
| (329,0,329) (330,1,329)
(12, 2, 329) (330,3,329) (None, '-', 329) |
329 330 12 330 None |
This gives rise to the following simple idea for checking the
correctness of a parse tree in some grammar G. A parse tree is always a
recursively defined list of nodes. A node N representing a non-terminal
has the structure N = [n, N1, N2, .... Nk] where n is the node id of N
and Ni are subsequent nodes. In order to check the structure it
suffices to check N° = [n, n1, ..., nk] the node id sequence of N and
each Ni recursively with terminals at the bottom of the recursion.
How to check N° ? We start by selecting the NFA corresponding to n and
the start label S = (n,
0, n).
Let T0 = {n01,n02,...,n0r}
be the label transitions of S. We keep the set Sel0 of projections of
the labels onto node ids. If n1 is not in Sel0 we know that N has a
corrupted structure in G. Otherwise we select the subset P01 of all
labels in T0 projecting onto n1. From the labels in P01 we create the
set of all label transitions T1 = {n11,n12,...,n1s}.
We repeat the ptocedure now with n2 and T1. The checking processes is
finished when we either reach node id nk or Ti is {(None,'-',n)}
for some i.
4.2 A first
trace based parser
A simple trace based parser is just slightly more complicated than the
parse tree checker we described in the last subsection. We start with a
token sequence tokenstream = [t1, ...., tn] being the result of lexical
analysis and an NFA N0 representing a top level rule of the grammar.
We apply the following parsing algorithm:
def parse(tokstream, nid, token):
nfa_trans
=
NFATracer(nid)
# select a NFATracer object for iterating through
# label transition sets of NFA[nid]
selection =
nfa_trans.get_selection(nid) # get
first selection of nids according to the
# label transitions of (nid, 0, nid)
parse_tree =
[nid]
# store nid as the top-level node in parse_tree
while
token:
# as long as token are available in the tokenstream...
for
s in
selection:
# iterate through node ids s of the selection
if s is not None:
if
is_token(s):
# if s is the node id of a terminal symbol and
if token_type(token) == s: # it
corresponds with the node id of the current token
tokstream.shift_right() # increment the read
position of the tokenstream
parse_tree.append(token) # and add the token to the
parse tree. We get
break
# parse_tree = [nid, ..., token] and terminate
# the for loop.
elif token_type(token) in first_set(s): # if s is the node
id of a non-terminal and
# if the node id of the current token is in the
# first_set of s we call parse recursively
P = parse(tokstream, s, token) # with s. The
result is a parse tree P
if
P:
# if P is not None add the parse tree to
parse_tree.append(res)
# parse_tree. We get parse_tree = [nid, ..., P]
break
else:
if None in
selection:
# there has not been a successfull non-None selection
return
parse_tree
# ... but that's o.k. if None is selectable
else:
raise
SyntaxError
# otherwise we failed to parse the tokenstream
selection = nfa_trans.get_selection(s)
# everything is o.k. now and we can demand the next
# selection in the current NFA from s
token =
tokstream.get_token()
# keep the next token. If there is no token left we
return
parse_tree
# are done
|
Note that get_selection(nid) works as described for the syntax checker.
There will always be a set L of lables stored by the NFATracer that
represents the internal state of the iteration through the NFA label
transitions. When get_selection(nid) is called following steps are made:
- determine the set S of all labels in L with L[0] == nid.
- get the transitions of each label in S and merge them to a
new label set L_next.
- build new selection = { label[0] for label in L_next} and
return it
4.3 NFA
expansions
In the algorithm described in 3.2 we made a significant simplification.
Once we have found a non-terminal containing the current token in its
first_set we call parse() again and if we can't parse the tokenstream
successfully we raise an error. It's not foreseen that another s in the
selection could be succefully applied. Indeed we demand that the
first_sets of the node ids in the selection are pairwise disjoint.
Seemingly this gives us little more than just an LL(1) parser. But this
impression is wrong.
That's because rules of the kind
S:
A B C ... i | A B C ... j | A B C ... k | ...
|
can be handled without problems. Although each A has a unique label and
defines an own trace all labels are projected onto the node id of A.
Suppose now we modify S:
S1: A1
B C ... i | A B C ... j | A B C ... k | ...
|
with A1 != A. The first_sets of A and A1 shall intersect. We can
substitue A1 and A by the productions defined on their right-hand-side.
After finitely many recursive expansions we reach one of two different
possible states:
- The expansion process runs into a cycle and can't be
terminated.
- We achieve the rule form of S with disjoint selections.
If we run in case 1. a warning will be flagged. This warning shall be
understood as a rejection of the grammar. In those cases Trail shall
not be used and the grammar shall be modified. This happens generally
with left recursive rules in grammars. Those can be somewhat hidden. We
will give an example at the end of the section.
The other more pressing problem is bookkeeping.
We can't simply replace A by its RHS in S because we need the node id
of A in the parse tree. So we need to keep track of A during
expansion.
4.3.1
Tracking of nodes during expansion
Keeping track of A when being expanded in S is quite cheap. A and S are
represented by their NFAs and a reference to A is in each label
(k, i,
A ) of A and a reference to S is in each label (l, j, S ) of
S. Since the labels are global data for a grammar G they can't ever be
confused. What's left is the treatment of the exit label (None, '-', A )
of A on embedding of A in S.
Embedding rules:
- Let (A,
k, S ) be the original label, we transform it into a new label
(
A, '.', k, S ). The dot argument indicates that this label
shall be skipped when selections are built. Instead on selection built
it is used by Trail to forward to its follow transition set. If the
follow transitions contain a dotted label the forwarding will continue.
- The dotted label ( A, '.', k, S ) replaces
(None,
'-', A ) in the transition set of A.
With those two rules we have all data being required to keep track on A
as well as a consistent embedding of A. The description of rule 1.
already mentions forwarding and forwarding makes parsing somewhat more
complicated because we cannot just build the parse tree within the
parse() function like we did above. That's because the dotted labels
which are skipped contain the necessary embedding information not being
available in the nid selections. The solution we apply is to
externalize the construction of the parse tree completely. In the above
algorithm the parse tree construction was expressed by simple list
definitions and extensions. We replace them by calls to so called NFAMultiTrace objects.
4.3.2
NFAMultiTrace objects
If anything in Trails design justifies the label trace based parsing it is the use of NFAMultiTrace
objects. A NFAMultiTrace object or short MTrace is a tree that grows in
intervals.
In the graphic below the growth principle is illustrated. Suppose A was
selected and the algorithm calls get_selection(A). The immediate follow
transitions are { (B, '.', 1, D), (B, '.', 1, C)}. The dotted labels
need
forwarding. The label (B, '.', 1, D) is forwarded to {(F, 6, D)} while
(B, '.', 1, C) if forwarded to a follow transition { (C, '.', 3, D)
} which needs
another forwarding that yields { (E1, 4, D) , (E2, 5, D) }. The MTrace
can grow now at any of the labels { (F, 6, D), (E1, 4, D) , (E2, 5, D)
}. The provided nid selection is (F,E) and the algorithm selects F.
Once F is
selected the MTrace can only grow in (F, 6, D). The available
transition becomes {(G, 7, D)}.
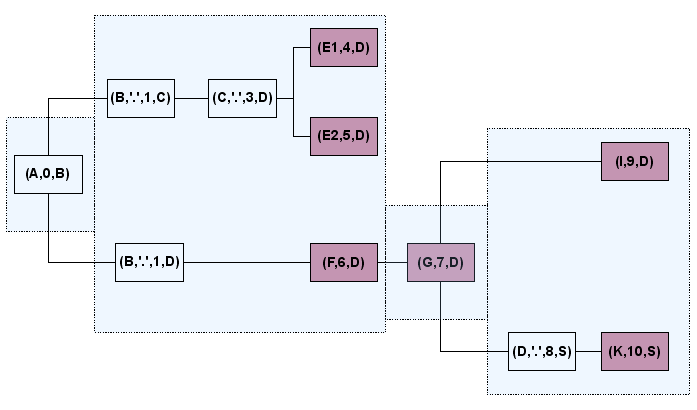
Suppose we reached the node (K, 10, 9) in our very last transition.
With (K,10, 9) we move along the parental chain back to (A, 0, B) and
get
( (K, 10, 9, S), (D, '.', 8, S), (G, 7, D), (F, 6, D), (B, '.', 1, D),
(A, 0, B) ). This flat trace can now be read in reverse order and
converted into a sequence of node ids which yields the final result (B
A D F G S K).
4.3.3
Drawbacks
Expansion can blow up the size of a single NFA notably. Below the
number of key labels of transitions are listed against the nodes
that are expanded.
|
Node
|
Nbr of Key Labels
|
unit
|
207
|
NUMBER
|
123
|
OPERATOR_DEF
|
86
|
Imagnumber
|
62
|
Floatnumber
|
40
|
STRING
|
26
|
Intnumber
|
15
|
The problem with current naïve implementation of Trail is that each of
those key labels can be a branch point in a NFAMultiTrace object. None
of these NFAMultiTraces grows strongly but the unit gets a hit quite
often. Also the selections are reconstructed each time. So we need
caching and access optimization techniques to reduce complexity of
Trail.
4.4
Features and Limitations of Trail
Notation. When we want
to embedd a rule A : RHS into another one S : A B ... we put A in
curlys i.e. S : {A : RHS} B ...
4.4.1
Dangling Else
The dangling-else rule is famous for its ambiguity:
Stmt:
'if' Expr 'then' Stmt | 'if' Expr 'then' Stmt 'else' Stmt
|
Suppose you expand the second branch of Stmt in the first branch...
| S:
'if' Expr 'then' {Stmt: 'if' Expr 'then' Stmt 'else'
Stmt } |
and compare this by expansion of the first branch of Stmt in the first
Stmt of the second branch
| S:
'if' Expr 'then' {Stmt: 'if' Expr 'then' Stmt } 'else'
Stmt |
How does Trail deal with it? Trail will always prefer the first
version. Only when Stmt after 'then' is fully parsed Trail will examine
whether it has to proceed ( move into the 'else' branch ) or terminate.
4.4.2
Case study : Django templates
Djangos template language syntax implements what I call extended braces. The following
example is kept from Djangos template documentation:
{% for story in story_list %}
<h2>
<a href="{{ story.get_absolute_url }}">
{{ story.headline|upper }}
</a>
</h2>
<p>{{ story.tease|truncatewords:"100" }}</p>
{% endfor %}
|
We attempt to encode this into the following rule...
| for_template_stmt:
'{%' 'for' expr 'in' expr '%}' stmt* '{%' 'endfor' '%}'
|
...and add two other rule descriptions:
stmt:
if_template_stmt | for_template_stmt | html_stmt
if_template_stmt: '{%' 'if' test '%}' stmt* '{%' 'endif' '%}'
|
Can you see the issue? When stmt* is entered Trail can either continue
parsing along '{%' 'endif' '%}' or it starts to parse another stmt that
might start with '{%' as well. Expansion leads to disambiguation here
but unfortunately we run into a cycle because we expand
if_template_stmt within itself.
5. Trace based
lexers
Prior to version 3.0 EasyExtend used a regular expression based
tokenization process. Actually EE's lexical analysis was just a
somewhat advanced modular version of stdlibs tokenizer.py algorithm.
The token defining parts as well as the regular expression building
were splitted into different modules. Even in EE 3.0 the basic
tokenization algorithm ( generate_tokens ) has just slightly changed.
It is still needed for the context sensitive parts of the Python
language: dealing with significant whitespace, line continuations,
comments and all other stuff that shall be ignored. However in EE 3.0
regular expression matching has been dropped and Trail is used instead.
5.1 Dropping
regular expressions
Building a regular expression for pattern matching is conceptually
simple. Just define a set
regular expressions {p1, p2, ..., pn}
- one for each token to be matched. Then concatenate those to
build a single big pattern p = p1| p2| ... |pn.
Now you can loop over a string, match string sections against p and do
some postprocessing. The drawback of this approach using Pythons
regular expression engine is that the result is not invariant under
permutations of the pattern pi.
In particular a simple transposition p' = p2| p1| ... |pn
can change the output dramatically.
Example: suppose you have
defined a pattern that recognizes floating point numbers
FLOAT: DEZIMAL '.' [DEZIMAL]
and another pattern that defines IPv4 addresses
IPv4: DEZIMAL '.' DEZIMAL '.' DEZIMAL '.' DEZIMAL
When you encode those patterns as regular expressions it
matters whether we execute IPv4|FLOAT
or FLOAT|IPv4.
In the first case IP addresses will be matched, while in the second
case it will be splitted into two floats and will never be matched.
5.2
Introduction to Litsets and Pseudo-Token
When we deal with the Lexer as just another parser the natural question
about the terminals of the Lexer arises. What are the TokenToken and
how do they fit into the parser architecture including NFA expansions?
5.2.1
Litsets
At the bottom level we have character sets and encodings. For sake of
simplicity the
first version of the Trail Lexer supports ASCII characters only for
encoding identifiers ( following Python 2.5 and not Python 3.0 ). So we
use them to encode
e.g. decimal or hexadecimal digit characters, but also whitespace etc.
|
Litset
|
Definition
|
LS_A_LINE_END
|
set(map(chr,[10,
13]))
|
LS_A_CHAR
|
set(string.ascii_letters+"_")
|
LS_A_WHITE
|
set(map(chr,[9,
10, 11, 12, 13, 32]))
|
LS_A_HEX_DIGIT
|
set(string.hexdigits)
|
LS_A_OCT_DIGIT
|
set(string.octdigits)
|
LS_A_NON_NULL_DIGIT
|
set('123456789')
|
LS_A_DIGIT
|
set(string.digits)
|
LS_A_BACKSLASH
|
set(['\\'])
|
LS_ANY
|
set()
|
Other characters being used occur explicitely in the Token file.
They play the same role as keywords in the Grammar file.
5.2.2
Pseudo-Token
Litsets are mapped one-one onto a a class of so called pseudo-token e.g. LS_A_WHITE
onto A_WHITE,
LS_A_ANY onto ANY
etc. There is no such thing as an initial token stream created by a
LexerLexer or Sublexer. So pseudo-token are token as-if. In case of
lexical analysis a pseudo-token simply matches a character when the
character is in the corresponding litset. An exception is made
with ANY. ANY is
characterized by the empty set but that's because we can't express the
notion of a set of all characters
in a comprehensive way. ANY is the
only pseudo-token that is handled explicitely in the parsing process.
We will discuss rules for ANY later.
There
is also a second class of pseudo-token that have no matching abilities
and corresponding character sets. Some of them are just present for
compliency with Pythons grammar but others are created explicitely in a
post lexing step. Those
are pseudo-token like T_INDENT,
T_DEDENT, T_ENDMARKER
or T_NEWLINE.
As a general rule A_
pseudo-token are used to match characters and T_
pseudo-token are for token streams being accepted by the parser.
5.2.2.1
pseudo-reachability
The implementation of NFAParser contains methods is_token
and is_reachable.
The first one simply checks whether a token is a terminal and the
latter checks if a symbol s is in parse_nfa.reachable[u]
for some other symbol u. These functions are substituted in the
lexer by is_pseudo_token
and is_pseudo_reachable.
The first one checks whether a symbol s is a key in the lex_nfa.pseudo_token
dictionary whereas the latter has following implementation
def is_pseudo_reachable(self, c, nid):
pseudo_token =
self.pseudo_reachable.get(nid)
if pseudo_token is None:
reach = self.lex_nfa.reachables.get(nid,[])
pseudo_token = [t for t in reach if self.is_pseudotoken(t)]
self.pseudo_reachable[nid] = pseudo_token
for t in pseudo_token:
if c in self.lex_nfa.pseudo_token[t]:
return True
return False
|
The
pseudo_reachable dictionary contains key-value pairs with nids as keys
and pseudo-token that are reachable from those nids as values. The
function iterates through the possible pseudo-token of the nid and
checks if the character parameter c is in the litset of one of
those pseudo-token. If so it returns True otherwise False.
5.2.3
Pseudo-Token expansion
What
happens when a character c is in the litset of two or more pseudo-token
in the previous algorithm? First come, first go. But this situation
shall not happen because it indicates that Trail has to select between
different alternative branches which are all promising - something
Trail isn't constructed for ( no backtracking, no more than 1 token of
lookahead ). So we have to make litsets of pseudo-token disjoint with respect to the
situation where a collision happens. This doesn't imply that the
litsets in lex_nfa.pseudo_token
were all disjoint.
Example: in the following
rule expression A_CHAR X |
A_HEX_DIGIT Y we have a collision between the
alphabetic characters used in the A_CHAR
litset and the same characters in the A_HEX_DIGIT
litset. So we create three sets: S1 = A_CHAR
/\ A_HEX_DIGIT, S2 = A_CHAR - A_HEX_DIGIT and
S3 =
A_HEX_DIGIT - A_CHAR. Now we can replace the above rule
expression by
S1 X | S1 Y | S2 X
| S3 Y
This disambiguation scheme suggests the following form of pseudo-token
expansion:
{A_CHAR:S1} X |
{A_HEX_DIGIT:S1} Y | {A_CHAR:S2} X | {A_HEX_DIGIT:S3} Y
5.2.4
Rules for ANY
ANY
interesects with everything and we have to take additional care for
values to the right of sequences of type ANY* or ANY+. When
matching symbols ANY has
always the weakest position among all characters and pseudo-token. So
we state following rule:
Rule for matching
with ANY: let S: ANY | B
be a rule and c a
character. If B can match c
then B will be selected as a matching rule.
Notice that this includes also None
as a matching rule. As a consequence a rule S: ANY*
would not match anything because the rule can always be terminated.
5.3 Can
your parser generator do this?

This rule is used to parse all variants of triple quoted strings with
double quotes " being possible in Python.
>>>
"""abc"""
'abc'
>>> """abc"def"""
'abc"def'
>>> """abc"def"geh"""
'abc"def"geh'
>>> """abc"def""geh"i"""
'abc"def""geh"i'
|
[1]
Recently I found a nice article
written
by Russ Cox about matching algorithms for regular
expressions which refers to an implementation method introduced by
Ken Thompson and published in 1968. The basic idea is very
similar to that used by Trail.
[2] When Trail parses Python these numerical
encodings
correspond to those being found in symbol.py and token.py of the
standard library.
|

